11 Modelo de Inversión
11.1 Descripción del Modelo
11.1.1 Introducción
Este modelo simula cómo las personas deciden en qué negocio invertir cuando las alternativas de inversión que se eligen difieren en sus ganancias anuales (profit) y en su riesgo de fracaso (risk). Estas alternativas comerciales (podía pensarse que son bancos) se van a modelar como parcelas.(Observe que este es un uso distinto a representar parcelas como espacios geograficos).
En esta primera versión, los inversores (agentes) perciben la información financiera de manera local, sólo de las parcelas vecinas (en posteriores versiones ampliaremos el “alcance” de los agentes).
11.1.2 Descripción del Modelo Odd Protocol
Especificaremos nuestro modelo de Negocio Simple usando el Protocolo ODD (RailsBack, Grimm), protocolo muy usado para especificar o definir MOBAs. La siguiente es la descripción ODD del modelo:
11.1.3 Objetivo del Modelo
El objetivo principal es explorar los efectos de la “Adquisición de Información” (qué información tienen los agentes y cómo la obtienen), y como se toman decisiones y se “adaptan” estas al utilizar la información adquirida. El modelo tiene que ver con decisiones de inversión, pero no pretende representar ningún enfoque de inversión real o sector empresarial, se podría considerar que este modelo representa aproximadamente a personas que compran y operan en negocios “locales”, en este caso los inversores están familiarizados con oportunidades de inversión dentro de un rango limitado (las parcelas vecinas) y asumiremos que seleccionar una alternativa de decisión de inversión no acarrea ningún costo (podría asemejarse por ejemplo a cambiar de banco).
11.1.4 Tipos de Agentes, Variables y escalas
Los agentes en este modelo son;
- Agentes inversores (tortugas) y
- Alternativas comerciales ó bancos (parcelas)
Las alternativas comerciales reciben dinero de sus clientes y varían en la ganancia que brindan a sus clientes y en el riesgo que tiene esa inversión; para ser específicos El Mundo es una cuadrícula de parcelas comerciales, cada uno de los cuales tiene dos variables:
- La ganancia anual que se proporciona allí (P, en unidades monetarias como dólares por año).
- el riesgo anual de que el negocio falle y el inversor pierda toda su riqueza (F, como probabilidad anual).
Los inversores tienen una riqueza actual (W, en unidades monetarias).
11.1.5 Escalas Espacio Temporales
- Escala de Espacio: El Mundo tiene un tamaño de 19 × 19 parcelas y tiene bordes.
- Escala de tiempo : los ticks corresponden a un año, y las simulaciones del modelo se realizaran por 50 años.
11.1.6 Procesos y ordenación temporal (scheduling)
El modelo incluye las siguientes acciones que se realizarán en el siguiente orden en cada tick:
Reposicionamiento: Los inversores deciden si un negocio similar (parcela adyacente) les ofrece una mejor opción que la actual; si es así, “reposicionan” y transfieren su inversión a esa parcela o banco, moviéndose allí. Solo un inversor puede ocupar un parcela a la vez.
Contabilidad. Los inversores actualizan sus variables de riqueza, estas se calculan incrementando la riqueza actual más el beneficio anual que le aporta la parcela (“banco” ) a donde se desplazó.
(Nota: El fracaso inesperado del negocio también está incluido en la acción contable. La variable F en las parcelas miden el riesgo de quiebra, en este caso el negocio falla y la riqueza W del inversor queda en cero, sin embargo el inversor permanece en el modelo)
11.1.7 Conceptos de diseño
Principios básicos. El tema básico de este modelo es cómo los agentes toman decisiones que involucran compensaciones (trade-offs) entre varios objetivos: en este caso aumentar las ganancias y disminuir el riesgo.
Emergencia: El resultado importante que se quiere mirar del modelo es que riqueza promedio tendrán los inversores luego de 25 años, tiempo en el cual se correrá el modelo
(Nota: Otros tipos de resultado podrían ser la máxima ganancia obtenida ó el número de inversores que han sufrido un fracaso. Estos resultados surgen de cómo los inversores individuales balancean (trade-off) sus beneficios y el riesgo involucrado, pero también del “clima de negocios”)
Comportamiento adaptativo. este es la decisión de a qué parcela vecina deben moverse (o quedarse en su parcela), considerando el beneficio y el riesgo de las diferentes alternativas. En esta versión del modelo, los inversores utilizan un sistema simplificado de análisis microeconómico para tomar su decisión, moviéndose a la parcela que proporciona el valor más alto de una función objetivo, que se describe a continuación.
Objetivo: En economía, el término “utilidad” se utiliza como sinónimo del objetivo que buscan los agentes, los inversores califican las alternativas mediante una medida de utilidad que represente su riqueza futura esperada al final de un horizonte temporal (T), en este caso se usaran “5 años”. Esta riqueza futura es una función de la riqueza actual y del riesgo que ofrece la alternativa. La función objetivo es la siguiente:
\[ U=(W+T.P)(1-F)^T \]
P: ganancia anual.F : probabilidad de riesgo.
W : riqueza del agente.
T: Horizonte (5 años).
Detección(Sensing): Los agentes inversores conocen la ganancia y el riesgo en la parcela donde se encuentra y en las parcelas vecinas adyacentes sin error.
Interacción. Los inversores interactúan entre sí indirectamente a través de la “competencia” por las parcelas:
- Un inversor no puede hacerse cargo de un negocio (pasar a una parcela) si está ya está ocupada por otro inversor.
- Los inversores ejecutan su acción de reposicionamiento en orden aleatorio, por lo que no hay preferencias (por ejemplo los inversores con mayor riqueza no tienen ventaja sobre otros)
Aleatoriedad (Estocasticidad) : El estado inicial del modelo es estocástico: los valores de P y F de cada parcela y las ubicaciones iniciales de los inversores, se establecen al azar (ver más adelante). No hay correlación entre ganancia y riesgo (P y F), son independientes.
11.1.8 Inicialización del modelo
Se utilizan cuatro parámetros del modelo para inicializar este mundo inversionista. Estos definen:
- Los valores de P Distribución Exponencial con media 5000.
- Los valores de F, Distribución Uniforme (desde 0.01 y 0.1).
- 100 agentes inversores se colocan en parcelas al azar en el mundo, evitando que dos invesores queden en una misma parcela. Las variable de riqueza W de cada inversor se colocan en cero.
11.1.9 Datos de entrada
No se utilizan datos de entrada.
11.1.10 Submodelos
- Reposicionamiento: Un agente identifica todas las empresas en las que podría invertir, las parcelas vecinas (ocho o menos si el agente está en el borde del mundo) que están desocupadas, más su parcela actual. El agente determina cuál de estas alternativas proporciona el valor más alto de función de utilidad,y se mueve a esta parcela (o permanece en su parcela si no hay una mejor utilidad en las parcelas vecinas).
*Contabilidad. Esta acción se describió en un apartado anterior (Procesos y ordenación temporal (scheduling)).
11.2 Construcción del Modelo
Abra Netlogo y Guarde el Archivo vacío como ModeloNegocio.nlogo
11.2.1 Configuración del Mundo:
Definiremos el mundo del Modelo de Negocio como un mundo de 19x19 parcelas con límites tanto horizontales como verticales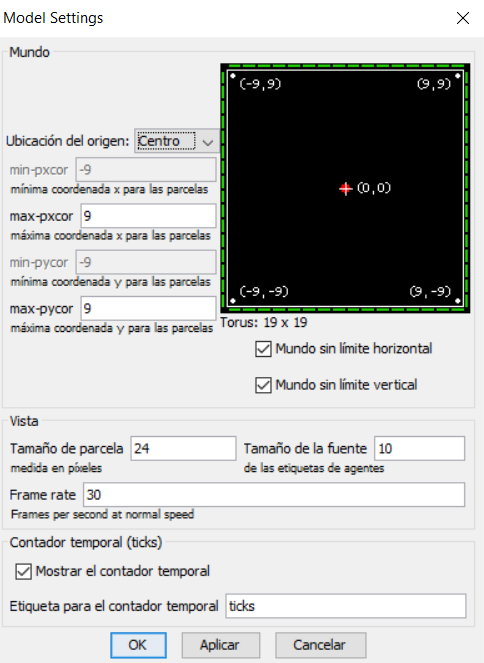
11.2.2 Procedimiento Setup
1. Modelación de las parcelas ( Bancos)
Cada parcela (banco) tendrá dos atributos asociados:
- la ganancia anual que ofrece esta parcela para los inversores
- El riesgo anual que tiene la inversión
patches-own
[
profit ; ganancia anual que da cada parcela (banco)
annual-risk ; ganancia anual que tiene cada parcela (banco)
]El procedimiento setup:
- limpia el mundo clear-all
- Configura las parcelas (bancos): procedimiento setup-patches.
- cronómetros en 0 : reset-ticks
to setup
clear-all
ask patches [setup-patches]
reset-ticks
end
to setup-patches
endsetup-patches (profit annual-risk):
El procedimiento setup-patches:
- Inicializa la ganancia anual de cada parcela (aleatorio entre 1000 y 10000)
- inicializa el riesgo de cada parcela (probabilidad entre 0.01 y 0.1)
to setup-patches
set profit random-exponential 5000
set risk 0.01 + random-float ( 0.1 - 0.01)
endPara una mejor visualización del modelo cada parcela mostrará:
- el riesgo como un número
- la utiilidad de color verde (entre más claro el verde, mayor la utilidad)
Estas dos lineas se añaden a setup-patches
set plabel (precision risk 2)
set pcolor scale-color green profit 1000 10000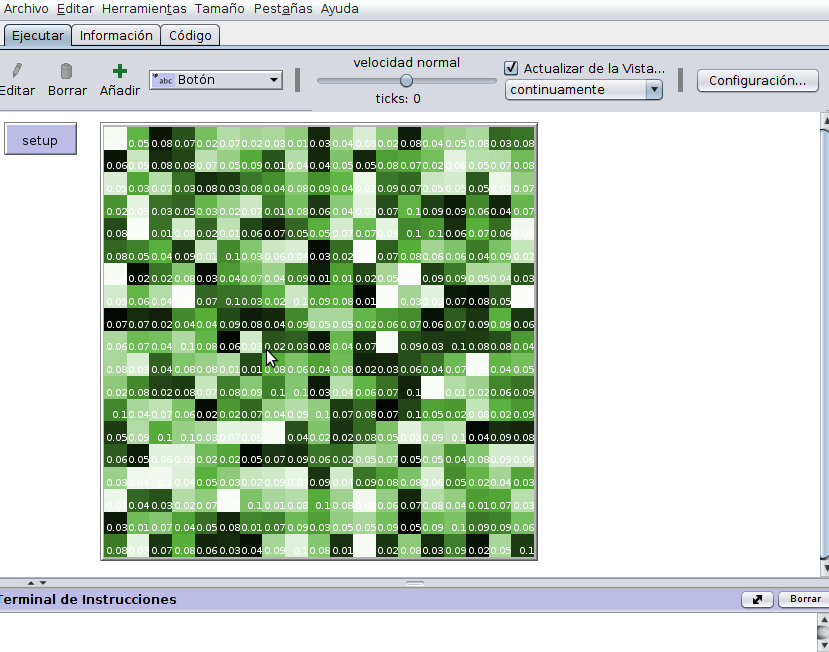
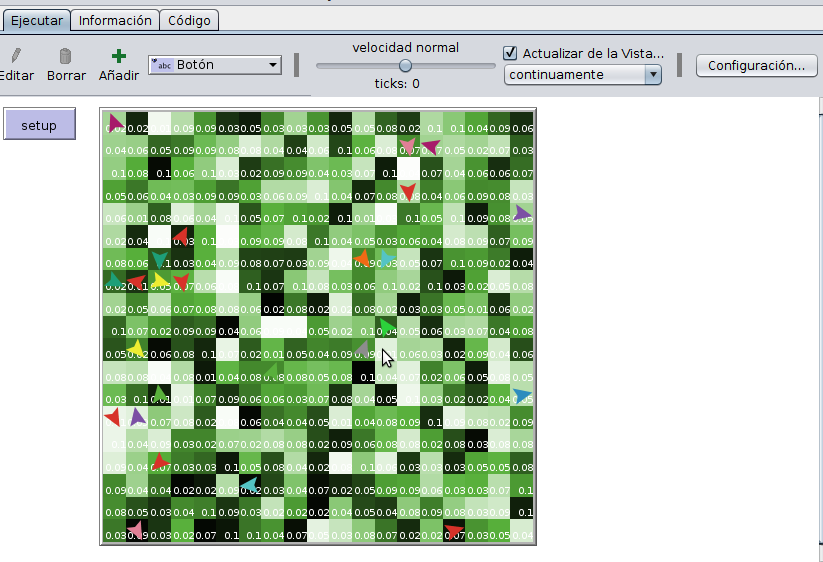
- Modelación de los agentes ( Inversores)
Añadir al setup la linea:
setup-inversoresy colocar debajo del setup:
to setup-inversores
endInicialmente se usaran 25 inversores, cada uno con un monto de dinero (wealth) inicialmente en 0:
Crear la variable global num-investors y la propiedad de riqueza (wealth) de los agentes, colocar en la parte superior de la pestaña de código lo siguente:
globals
[
num-investors ; variable global número de inversores
]
turtles-own
[
wealth ; riqueza de l agente inicialmente en cero
]Definir dentro de setup el número de inversores:
set num-investors 25y ahora colocar dentro de setup-inversores lo siguiente:
create-turtles num-investors
[
move-to one-of patches with [not any? turtles-here] ; ocupen una parcela no ocupada!!!!
set wealth 0.0 ; riqueza en cero
pen-down ; activar rastro de agentes para observar su trayectoria
]
globals
[
num-investors ; variable global número de inversores
]
turtles-own
[
wealth ; riqueza de l agente inicialmente en cero
]
patches-own
[
profit ; ganancia anual que da cada parcela (banco)
risk ; ganancia anual que tiene cada parcela (banco)
]
to setup
clear-all
set num-investors 25
ask patches [setup-patches]
setup-inversores
reset-ticks
end
to setup-patches
set profit 1000 + random ( 10000 - 1000 ) ; profit entre 1000 y 10000
set risk 0.01 + random-float ( 0.1 - 0.01 ) ; risk entre 0.01 y 0.1
; para visualización
set plabel precision risk 2 ; visualizar numéricamente el riesgo en cada
set pcolor scale-color green profit 1000 10000 ; visualizar por color la ganancia
; verde más claro más ganancia
end
to setup-inversores
create-turtles num-investors
[
move-to one-of patches with [not any? turtles-here] ; ocupen una parcela no ocupada!!!!
set wealth 0.0 ; riqueza en cero
pen-down ; activar rastro de agentes para observar su trayectoria
]
end
11.2.3 Procedimiento Go
Lo primero es determinar cuando el modelo se detiene (para), usaremos una variable global llamada years-simulated:
globals
[
num-investors ; variable global número de inversores
years-simulated ; número de años en que el modelo se va a correr
]inicializamos en el setup la variable years-simulated:
set years-simulated 50y construimos la primera versión del procedimiento go:
to go
if ticks >= years-simulated [stop]
tick
end
Antes de continuar debemos acordarnos que el cálculo de la utilidad de un agente: \[ U=(W+T.P)(1-F)^T \]
requiere de un “horizonte-de-tiempo” T, que nos dará el horizonte de tiempo en el que estamos considerando la inversión, entonces la definiremos como variable global:
globals
[
num-investors ; variable global número de inversores
years-simulated ; número de años en que el modelo se va a correr
time-horizon ; horizonte de tiempo paara el calculo de la utilidad
]el valor que le daremos a esta variable es 5 años, coloquemos en el setup la siguiente linea:
set time-horizon 5 ; horizonte de tiempo 5 añosAhora si podemos continuar, El procedimiento go va a tener dos subprocedimientos:
reposition: determina cual parcela, no ocupada , vecina me proporciona mejor inversión para moverme a ella (en caso de que no exista esa mejor parcela me quedo quieto.
do-accounting: una vez me muevo actualizo mi dinero (wealth)
Para determinar que inversión es la mejor debo calcular para cada parcela vecina no ocupada la utilidad de la inversión, para ello definiremos un reporter (que usaran las parcelas) que hace esta cálculo dado un agente (que tiene determinada cantidad de dinero), el reporter es el siguiente:
to-report utilidad-para [un-inversor]
let riqueza-inversor [wealth] of un-inversor ; riqueza del inversor
let utilidad
riqueza-inversor + (profit * time-horizon) * ((1 - risk) ^ time-horizon)
; aplica fórmula de utilidad al inversor
report utilidad ; reporta la utilidad
endFinalmente definamos las funciones : reposition y do-accounting.
coloquemos en el go lo siguiente, antes de tick:
ask turtles [reposition]
ask turtles [do-accounting]
y definamos estos dos procedimientos:
to reposition
let potential-destinations neighbors with [not any? turtles-here]
set potential-destinations (patch-set potential-destinations patch-here)
let best-patch max-one-of potential-destinations [utility-for myself]
move-to best-patch
end
to do-accounting
set wealth (wealth + profit) ; Primero , añada ganancia anual
if random-float 1.0 < risk ; Mire si la inversión quiebra
[
set wealth 0
]
endEl texto completo del go es el siguiente:
to go
if ticks >= years-simulated [stop]
ask turtles [reposition]
ask turtles [do-accounting]
tick
end
to reposition
let potential-destinations neighbors with [not any? turtles-here]
set potential-destinations (patch-set potential-destinations patch-here)
let best-patch max-one-of potential-destinations [utilidad-para myself]
move-to best-patch
end
to do-accounting
set wealth (wealth + profit) ; Primero , añada ganancia anual
if random-float 1.0 < risk ; Mire si la inversión quiebra
[
set wealth 0
]
end
to-report utilidad-para [un-inversor]
let riqueza-inversor [wealth] of un-inversor ; riqueza del inversor
let utilidad
riqueza-inversor + (profit * time-horizon) * ((1 - risk) ^ time-horizon)
; aplica fórmula de utilidad al inversor
report utilidad ; reporta la utilidad
end
El texto completo del modelo es el siguiente:
globals
[
num-investors ; variable global número de inversores
years-simulated ; número de años en que el modelo se va a correr
time-horizon ; horizonte de tiempo paara el calculo de la utilidad
]
turtles-own
[
wealth ; riqueza de l agente inicialmente en cero
]
patches-own
[
profit ; ganancia anual que da cada parcela (banco)
risk ; ganancia anual que tiene cada parcela (banco)
]
to setup
ca
set num-investors 25
set years-simulated 50
set time-horizon 5
ask patches [setup-patches]
setup-inversores
reset-ticks
end
to setup-inversores
crt num-investors
[
move-to one-of patches with [not any? turtles-here]
set wealth 0.0
pen-down
]
end
to setup-patches
set profit random-exponential 5000
set risk 0.01 + random-float ( 0.1 - 0.01)
set plabel (precision risk 2)
set pcolor scale-color green profit 1000 10000
end
to go
if ticks >= years-simulated [stop]
ask turtles [reposition]
ask turtles [do-accounting]
tick
end
to reposition
let potential-destinations neighbors with [not any? turtles-here]
set potential-destinations (patch-set potential-destinations patch-here)
let best-patch max-one-of potential-destinations [utilidad-para myself]
move-to best-patch
end
to do-accounting
set wealth (wealth + profit) ; Primero , añada ganancia anual
if random-float 1.0 < risk ; Mire si la inversión quiebra
[
set wealth 0
]
end
to-report utilidad-para [un-inversor]
let riqueza-inversor [wealth] of un-inversor ; riqueza del inversor
let utilidad
riqueza-inversor + (profit * time-horizon) * ((1 - risk) ^ time-horizon)
; aplica fórmula de utilidad al inversor
report utilidad ; reporta la utilidad
endFinalmente coloquemos un botón go y corramos el modelo:
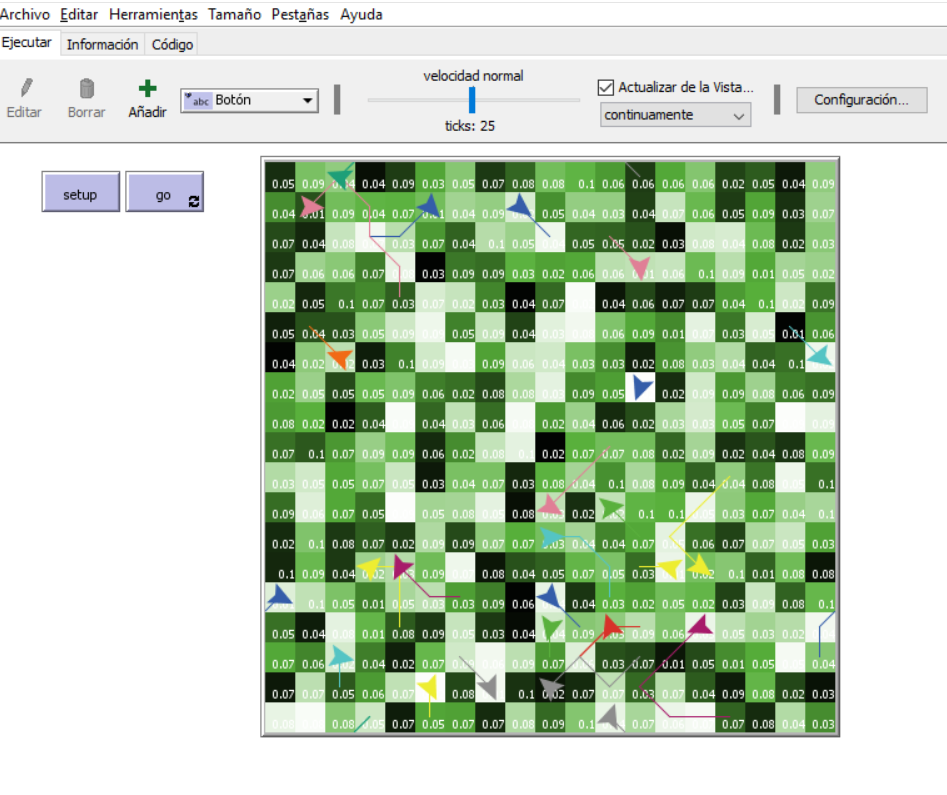
El modelo lo puede correr en el siguiente applet: